proximal_box_constraint

odl.solvers.nonsmooth.proximal_operators.proximal_box_constraint(space, lower=None, upper=None)[source]

Proximal operator factory for G(x) = ind(a <= x <= b).

If P is the set of elements with a <= x <= b, the indicator function of which is defined as:

ind(a <= x <= b) = {0 if x in P, infinity if x is not in P}

with x being an element in space.

Parameters:
spaceLinearSpace

Domain of the functional G(x)

lowerspace.field element or space element-like, optional

The lower bound. Default: None, interpreted as -infinity

upperspace.field element or space element-like, optional

The upper bound. Default: None, interpreted as +infinity

Returns:
prox_factoryfunction

Factory for the proximal operator to be initialized

See also

proximal_nonnegativity

Special case with lower=0, upper=infty

Notes

If 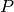P is an interval [a,b], the indicator function is defined as

I_{P}(x) = \begin{cases} 0 & \text{if } x \in P, \\ \infty & \text{if } x \not \in P \end{cases}

For a step size 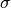\sigma, the proximal operator of \sigma I_{P} is given by the projection onto the interval

\mathrm{prox}_{\sigma I_{P}}(x) = \begin{cases} a & \text{if } x < a, \\ x & \text{if } x \in [a,b], \\ b & \text{if } x > b. \end{cases}

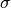The proximal operator is independent of \sigma and invariant under a positive rescaling of I_{P}(x), since that leaves the indicator function unchanged.

For spaces of the form R^n, the definition extends naturally in each component.