admm_linearized¶

odl.solvers.nonsmooth.admm.admm_linearized(x, f, g, L, tau, sigma, niter, \*\*kwargs)[source]¶

Generic linearized ADMM method for convex problems.

ADMM stands for “Alternating Direction Method of Multipliers” and is a popular convex optimization method. This variant solves problems of the form

min_x [ f(x) + g(Lx) ]

with convex f and g, and a linear operator L. See Section 4.4 of [PB2014] and the Notes for more mathematical details.

Parameters

xL.domain element: Starting point of the iteration, updated in-place.
f, gFunctional: The functions f and g in the problem definition. They need to implement the proximal method.
Llinear Operator: The linear operator that is composed with g in the problem definition. It must fulfill L.domain == f.domain and L.range == g.domain.
tau, sigmapositive float: Step size parameters for the update of the variables.
niternon-negative int: Number of iterations.

Other Parameters

callbackcallable, optional: Function called with the current iterate after each iteration.

Notes

Given $x^{(0)}$ (the provided x) and $u^{(0)} = z^{(0)} = 0$ , linearized ADMM applies the following iteration:

$x^{(k+1)} &= \mathrm{prox}_{\tau f} \left[ x^{(k)} - \sigma^{-1}\tau L^*\big( L x^{(k)} - z^{(k)} + u^{(k)} \big) \right] z^{(k+1)} &= \mathrm{prox}_{\sigma g}\left( L x^{(k+1)} + u^{(k)} \right) u^{(k+1)} &= u^{(k)} + L x^{(k+1)} - z^{(k+1)}$

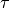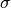The step size parameters $\tau$ and $\sigma$ must satisfy

$0 < \tau < \frac{\sigma}{\|L\|^2}$

to guarantee convergence.

The name “linearized ADMM” comes from the fact that in the minimization subproblem for the 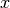$x$ variable, this variant uses a linearization of a quadratic term in the augmented Lagrangian of the generic ADMM, in order to make the step expressible with the proximal operator of $f$ .

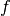Another name for this algorithm is split inexact Uzawa method.

References

[PB2014] Parikh, N and Boyd, S. Proximal Algorithms. Foundations and Trends in Optimization, 1(3) (2014), pp 123-231.