GroupL1Norm¶

class odl.solvers.functional.default_functionals.GroupL1Norm(*args, **kwargs)[source]¶

The functional corresponding to the mixed L1-Lp norm on ProductSpace.

The L1-norm, || ||x||_p ||_1, is defined as the integral/sum of ||x||_p, where ||x||_p is the pointwise p-norm.

This is also known as the cross norm.

Notes

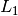If the functional is defined on an $\mathbb{R}^{n \times m}$ -like space, the group $L_1$ -norm, denoted $\| \cdot \|_{\times, p}$ is defined as

$\|F\|_{\times, p} = \sum_{i = 1}^n \left(\sum_{j=1}^m |F_{i,j}|^p\right)^{1/p}$

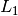If the functional is defined on an $(\mathcal{L}^p)^m$ -like space, the group $L_1$ -norm is defined as

$\| F \|_{\times, p} = \int_{\Omega} \left(\sum_{j = 1}^m |F_j(x)|^p\right)^{1/p} \mathrm{d}x.$

Attributes:

Methods

`__call__`(x[, out])	Return `self(x[, out, **kwargs])`.
`bregman`(point, subgrad)	Return the Bregman distance functional.
`derivative`(point)	Return the derivative operator in the given point.
`norm`([estimate])	Return the operator norm of this operator.
`translated`(shift)	Return a translation of the functional.

__init__(vfspace, exponent=None)[source]¶

Initialize a new instance.

Parameters:

vfspaceProductSpace: Space of vector fields on which the operator acts. It has to be a product space of identical spaces, i.e. a power space.
exponentnon-zero float, optional: Exponent of the norm in each point. Values between 0 and 1 are currently not supported due to numerical instability. Infinity gives the supremum norm. Default: vfspace.exponent, usually 2.

Examples

>>> space = odl.rn(2)
>>> pspace = odl.ProductSpace(space, 2)
>>> op = GroupL1Norm(pspace)
>>> op([[3, 3], [4, 4]])
10.0

Set exponent of inner (p) norm:

>>> op2 = GroupL1Norm(pspace, exponent=1)
>>> op2([[3, 3], [4, 4]])
14.0