RealPart.adjoint¶

property RealPart.adjoint¶

Return the (left) adjoint.

Notes

Due to technicalities of operators from a complex space into a real space, this does not satisfy the usual adjoint equation:

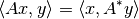
$\langle Ax, y \rangle = \langle x, A^*y \rangle$

Instead it is an adjoint in a weaker sense as follows:

$\langle AA^*x, y \rangle = \langle A^*x, A^*y \rangle$

Examples

The adjoint satisfies the adjoint equation for real spaces:

>>> r3 = odl.rn(3)
>>> op = RealPart(r3)
>>> x = op.domain.element([1, 2, 3])
>>> y = op.range.element([3, 2, 1])
>>> x.inner(op.adjoint(y)) == op(x).inner(y)
True

If the domain is complex, it only satisfies the weaker definition:

>>> c3 = odl.cn(3)
>>> op = RealPart(c3)
>>> x = op.range.element([1, 2, 3])
>>> y = op.range.element([3, 2, 1])
>>> AtAxy = op(op.adjoint(x)).inner(y)
>>> AtxAty = op.adjoint(x).inner(op.adjoint(y))
>>> AtAxy == AtxAty
True