ComplexModulusSquared.derivative¶

ComplexModulusSquared.derivative(x)[source]¶

Return the derivative operator in the "C = R^2" sense.

The returned operator (self) is the derivative of the operator variant where the complex domain is reinterpreted as a product of two real spaces.

Parameters:

xdomain element: Point in which to take the derivative.

Notes

The derivative of the squared complex modulus

$&S: X(\mathbb{C}) \to X(\mathbb{R}), \\ &S(x) = 2\Re(x)^2 + \Im(x)^2,$

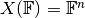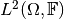with $X(\mathbb{F}) = \mathbb{F}^n$ or $L^2(\Omega, \mathbb{F})$ , is given as

$&S'(x): X(\mathbb{C}) \to X(\mathbb{R}), \\ &S'(x)(y) = 2(\Re(x)\,\Re(y) + \Im(x)\,\Im(y)).$

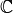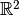It is linear when identifying $\mathbb{C}$ with $\mathbb{R}^2$ , but not complex-linear.

Examples

>>> c2 = odl.cn(2)
>>> op = odl.ComplexModulusSquared(c2)
>>> op([3 + 4j, 2])
rn(2).element([ 25.,   4.])
>>> deriv = op.derivative([3 + 4j, 2])
>>> deriv.domain
cn(2)
>>> deriv.range
rn(2)
>>> deriv([2 + 1j, 4j])  # [(3*2 + 4*1) * 2, (2*0 + 0*4) * 2]
rn(2).element([ 20.,   0.])